It’s a seemingly easy problem: how to make a certain amount of money using the smallest number of coins possible. For example, 42p needs three coins: a couple of twenty pence pieces and a 2p coin. It’s something that comes up on the maths national curriculum:

Y3: Pupils continue to become fluent in recognising the value of coins, by …  giving change using manageable amounts.

It’s also something that machines need to be programmed to do – from snack vending machines to automated checkouts. The lesson here looks at how a computer could be programmed to give arbitrary amounts of change.

Objectives

• Practice working out the smallest set of coins to give change
• Work out an algorithm for giving change and check this works
• Use sequence, repetition, variables and input and output to program this using a block-based language such as Scratch
• Test and debug the program
• Look for ways to improve the program using patterns.

Starter

Check pupils’ knowledge of coins by making sure the class know all the standard UK coins. Pupils who’ve been abroad might like to discuss the coinage systems in other countries.

Get pupils thinking about the problem of making change by asking quick-fire questions, ranging from the easy (What coins make 13p?) to the more challenging (What coins make 48p? What coins make £2.88?). Do pupils’ answers use the smallest number of possible coins?

Main activities

Start with computational thinking before getting on to any hands-on coding work. Explain that lots of machines have to solve the problem of making change: what machines can pupils think of that might need to do this? Why might it be annoying if the machines didn’t give the smallest number of coins?

To program machines to do this, we first need to think of an algorithm – the sequence of steps – that would solve this problem. Get pupils to work with a partner to brainstorm ideas for their algorithm, encouraging them to write these down. Pupils should test each other’s algorithms, working through the steps they’ve listed. Do they work for any amount of money? If not, pupils will need to refine their ideas.

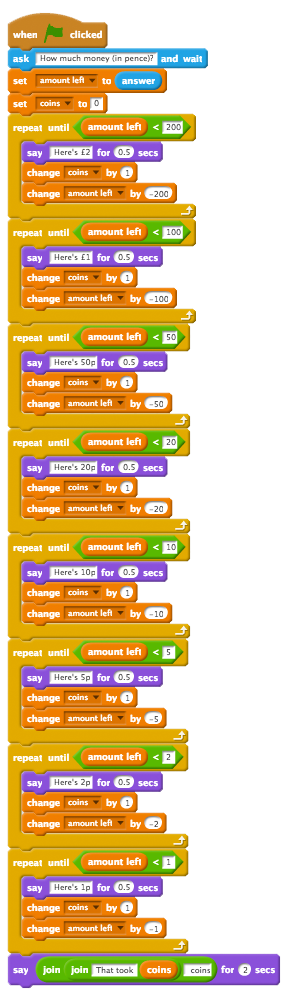
A typical algorithm might be:

• Start with the total amount, and no coins in the change.
• Repeat until amount left is less than £2:
  • Subtract £2 from the amount; add £2 to the change.
• Repeat until amount left is less than £1:
  • Subtract £1 from the amount; add £1 to the change.
• Repeat until amount left is less than 50p:
  • Subtract 50p from the amount; add 50p to the change.
• Repeat until amount left is less than 20p:
  • Subtract 20p from the amount; add 20p to the change.
• Repeat until amount left is less than 10p:
  • Subtract 10p from the amount; add 10p to the change.
• Repeat until amount left is less than 5p:
  • Subtract 5p from the amount; add 5p to the change.
• Repeat until amount left is less than 2p:
  • Subtract 2p from the amount; add 2p to the change.
• Repeat until amount left is less than 1p:
  • Subtract 1p from the amount; add 1p to the change.

Point out a couple of things about this algorithm to your pupils. Firstly, that this is what we call a ‘greedy’ algorithm: at each step we take off the largest amount we can. Secondly, there’s a pattern here, and that’s something which we might be able to use if we wanted to write our algorithm in a clearer or more compact.

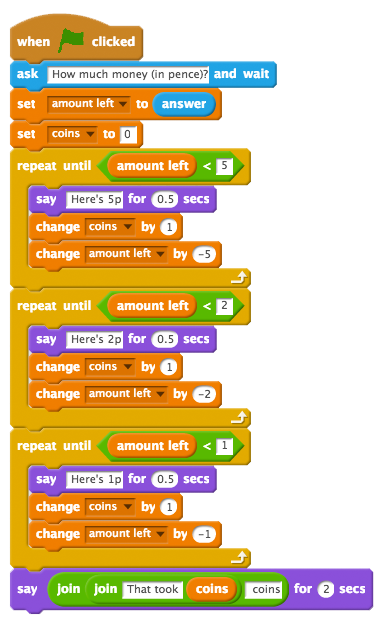
Once pupils have an algorithm that works, either their own or one you’ve shared with them, they can program this into Scratch (or another programming language). You’ll need to explain a few ideas here, or just remind them of these. You might like to give them a partially complete program (e.g. one that works for only 1p, 2p and 5p coins) and ask them to complete it:

Or you could walk through the steps as a class, or you could just remind them of a few key ideas: it depends on how much experience your pupils have already.

• We’ll need a couple of variables to keep track of the amount left and the number of coins so far, so in Scratch, click the orange palette and create a couple of variables, say ‘amount’ and ‘coins’. Drag set coins to 0 into the script window to initialise this.
• To initialise the amount, we’ll use keyboard input from our user, so on the blue sensing palette use the ‘ask… and wait’ block to prompt the user for an amount of money, and then use then set our amount variable to the answer they give.
• For each of the possible coins we’ll give in change, the pattern will be the same: use a repeat until block to check if the amount is less than the value of the coin (say 200 in the first case). Inside the block, change the amount variable by the value of the coin, i.e. -200 in this case, and increase the coins variable by 1. It’s nice to output something on screen here, so use a say block from the purple palette to say ‘Here’s a £2 coin’ or something like this for a second or so. You, or your pupils, then just need to follow the same pattern for all the other coins, until you get down to 1p.
• The last bit of the program should be to say how many coins were given in total, combining the purple say for and the orange coins variable block.

Provide pupils with the time to work through this. Having pupils work with a partner can be a really effective approach, both to writing code and to learning to write code.

Make sure pupils test their programs for different starting amounts, and do give pupils some strategies for debugging their code if things don’t go to plan – one approach is to put themselves in the place of the computer, carrying out the program ‘by hand’.

There’s a simple solution to the problem online which you’re free to remix and / or share with your pupils.

Extension ideas

Can pupils improve their program, making it clearer or more elegant? Using so many similar repeating blocks suggests a couple of ways to make this better: one would be to use would be to break out the blocks that are repeated here into custom (purple) blocks in Scratch, another would be to use lists of possible coins, and perhaps keep a list of the coins we’ve given in change.

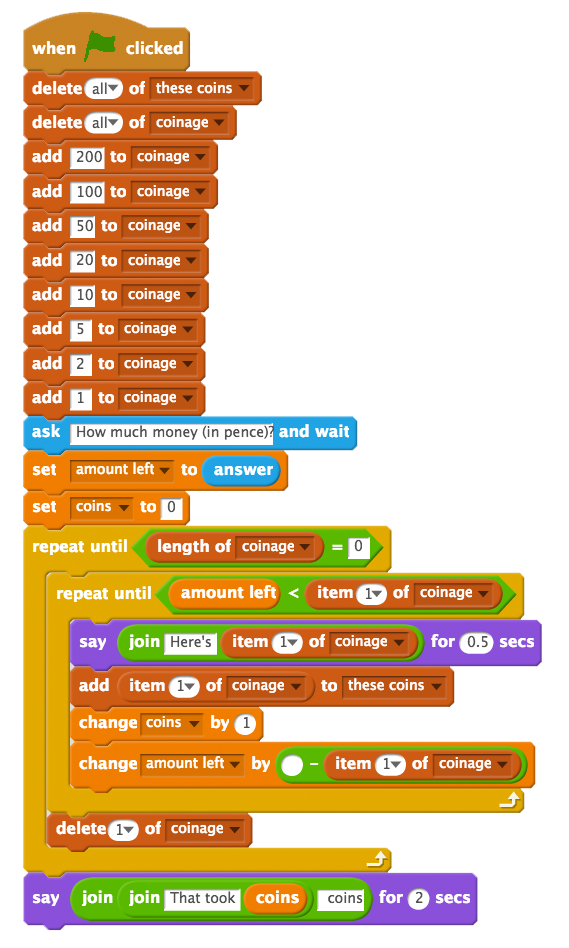
Our greedy algorithm here can break down in odd coinage systems (for example, use a coinage system with 25p, 20p, 10p and 5p coins to make change for 40p). You could challenge pupils to experiment with their program to see if they could find coinage systems where the algorithm didn’t work.

A much harder activity is to work out how many possible ways there are to make a given amount of change: for example there are 451 ways to make 50p using UK coinage!

The above lesson plan was published in the November 2016 edition of Teach Primary from Teachwire. © all rights reserved.